NOVENO GRADO

OPERACIONES ENTRE REALES 

POTENCIACIÓN 

Es importante que recuerdes las propiedades de la potenciación
 

 

Los exponentes se utilizan en casi todas las ramas de las matemáticas, desde álgebra básica hasta variable compleja. Observa los siguientes ejemplos básicos.

a) resolverlo Dado el siguiente sistema de dos ecuaciones lineales: 2 x + y =3

3/2 x - 2 y = 5

 

 

 

FACTOR COMÚN

Se dice que un polinomio tiene factor común cuando una misma cantidad, ya sea número o letra, se encuentra en todos los términos del polinomio.

Si en todos los términos de un polinomio figura un factor común, dicho polinomio es igual al producto de ese factor por el polinomio que resulta al dividir cada término por ese factor.

Para efectuar el factor común hay que tomar en cuenta que este se realiza tanto para los números como para las letras, y con las letras se toma la que tenga el menor exponente de todas.

 

Ejemplo:

 

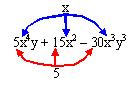
Como puede verse el cinco es el común numérico y la “x” la única letra común en este polinomio, como dos es el menor exponente de “x” es este el exponente que se tomara en cuenta, siendo el factor común 5x2.
Nos queda como respuesta:

 

 

Ejemplos:
Encontrar el factor común de los siguientes términos:

 

 

 

 

 

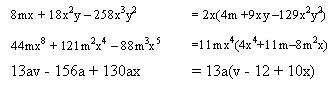
por cualquier método numérico (igualación. Sustitución, reducción o determinantes)

b) Resolverlo gráficamente

 

La suma de un número más el triplo de otro es igual a 17. Si al triplo del primero se resta el duplo del segundo, se obtiene 7. ¿Cuáles son los números?

 

Resolver la ecuación: (x + 1) / (x – 1) – (x – 1) / (1 + x) + 1 / x² = 0

 

Resolver: a) (Ö x + Öy) (Öx - Öy) = b) Öx - Öy² =

 

Calcular el valor numérico de ambas expresiones anteriores para x = 9; y = 4

 

Calcular y expresar el resultado en notación científica:

 

(3,2 . 10¹⁷ ) . ( 0,000000067) =

(2,487 . 10¹² ) . (2,8 . 10^-5 )

 

Desde lo alto de un poste de 6 m de altura, se tiende un cable recto hasta un punto del suelo situado a 8 m de la base del poste (Dibujarlo). A) ¿Cuál es el largo del cable? B) ¿Qué ángulo forma el cable con el suelo?

1) REDUCCION DE RADICALES SEMEJANTES

Reducir los siguientes radicales:

a) √6 + 5√6 - 12√6

b) 1/4√3 + 2/5√3

c) ( X-1)√5 + (X -4)√5 + (X – 6)√5

d) 4x√y + 10x√y - 12x√y

e) a√x + 6a√x + 9a√x - 7a√x

f) x√a² + 3x√a² - 8x√a²

 

2) SUMA Y RESTA DE RADICALES

a) √45 + √33 - 2√20

b) 1/7√147 – 1/5√700 + 1/10√28

c) 3√108 +1/10√625 +1/7√175

d) 5√48 - 3√36 + 2√384 + 4√81

e) √40 +√1029 -√625

f) 6√300 + 95√100 -25√36

3) MULTIPLICACION DE RADICALES DEL MISMO INDICE.

a) 3√45 x 1/6√15 x. 4√20

b) x√5a x 6a√8a

c) 3/4√6a ² x 8√4a ²

 d) 3√6 x 5√4 x 2√35

e) 4/5√15 x 5/6√50 f) 6√21 x 3√3

 

4) MULTIPLICACION DE RADICALES DE DISTINTO INDICE

a) √x por √2x³

b) 4√2ab por 7√8a ³

c) 4/5√4m² por7/2√16m⁴n

d) √2/x por √x⁴

e) √25x⁴ por √12x²

f) 4/3√5m²y por 5/6√9m³y

 

5) RADICALES COMPUESTOS

MULTIPLICAR: a) 5√x – 2 por √x

b) √x+1 + 2√x por 3√x+1 - √

c) 7√5 - 11√7 por 5√5 - 8√7

d) 2√a - 3√a-b por 3√a + √a-b

e) √a - 2√x por 3 √a + √x

6) DIVISION DE RADICALES DEL MISMO INDICE

a) 8√10 ÷ 2√5

b) √75x²Y³ ÷ 5√3XY

c) 2a/3√x³ ÷ a/3x²√x²

d) 5/6√1/2 ÷ 10/3 √2/3

e) 3√16a ⁵ ÷ 4 √2a ^2.

7) DIVISION DE RADICALES DE DISTINTO INDICE

a) √4a ² ÷ √2a

b) √9x⁴ ÷ √3x ²

c) 4/5 √4ab ÷ 1/10 √2a ²

d) √3m⁴ ÷ √ 27m²

e) √2 ÷ √2.

8) POTENCIA DE RADICALES.

a) (4√2)²

b) ( 2 √4 )²

c) ( √ 2 - √3)²

d) ( 4a √2x)²

e) ( 5√7 – 6 )²

9) RACIONALIZACION

Racionalizar el denominador de:

a) 3/√2x

b) 1/√3

c) 3/4√5

d) 6/5√ 3x

e) 5n²/3√mn

 

 

 

FACTORIZACIÓN

Antes de comenzar directamente con los casos de factoreo vamos a necesitar algunas  definiciones:

Factor:           Cuando un polinomio se escribe como producto de otros polinomios,
cada polinomio del producto es un factor del polinomio original.

Factorización: es el proceso con el cual expresamos un polinomio como un producto.

Primo:             Se dice que un polinomio es primo o irreducible cuando no puede 
escribirse como producto de dos polinomios de grado positivo.

Al factorizar un polinomio el objetivo es expresarlo como un producto de polinomios primos o potencias de polinomios primos, tratando principalmente de trabajar con los números enteros.

La factorización juega un papel importante en una gran cantidad de aplicaciones de la matemática, pues nos permite convertir expresiones muy complicadas en expresiones más simples facilitando así su estudio.

Para facturar un monomio se realiza por pura inspección, separando lo números y las letras entre si.

 

Prueba general de los factores

En cualquiera de los casos de factores la prueba es la misma multiplica los polinomios primos para ver si el resultado es el polinomio original.

 

 

 

FACTOR COMÚN

Se dice que un polinomio tiene factor común cuando una misma cantidad, ya sea número o letra, se encuentra en todos los términos del polinomio.

Si en todos los términos de un polinomio figura un factor común, dicho polinomio es igual al producto de ese factor por el polinomio que resulta al dividir cada término por ese factor.

Para efectuar el factor común hay que tomar en cuenta que este se realiza tanto para los números como para las letras, y con las letras se toma la que tenga el menor exponente de todas.

 

Ejemplo:

 

Como puede verse el cinco es el común numérico y la “x” la única letra común en este polinomio, como dos es el menor exponente de “x” es este el exponente que se tomara en cuenta, siendo el factor común 5x2.
Nos queda como respuesta:

 

 

Ejemplos:
Encontrar el factor común de los siguientes términos:

 

 

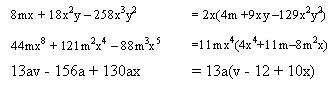
FACTOR COMÚN POR AGRUPACION DE TERMINOS

 

Se llama factor común por agrupación de términos, si los términos de un polinomio pueden reunirse en grupos de términos con un factor común diferente en cada grupo.

Cuando pueden reunirse en grupos de igual número de términos se le saca en cada uno de ellos el factor común. Si queda la misma expresión en cada uno de los grupos entre paréntesis, se la saca este grupo como factor común, quedando así una multiplicación de polinomios.

Tratar desde el principio que nos queden iguales los términos de los paréntesis nos hará mas sencillo el resolver estos problemas.

                        2ax + 2bx - ay + 5a - by + 5b

Agrupo los términos que tienen un factor común

                        (2ax - ay + 5a ) + ( 2bx - by + 5b )

Saco el factor común de cada grupo

                        a ( 2x - y + 5 ) + b (2x - y + 5 )

Como las expresiones encerradas entre paréntesis son iguales se tiene:

                        ( 2x -y +5 )(a + b)

Que es nuestra respuesta.

Ejemplos:

17ax – 17mx + 3ay - 3my + 7az – 7mz           = a(17x +3y +7z) - m(17x + 3y +7z)
                                                                         = (17x +3y +7z)(a – m)

 

m(x + 2) – x – 2 + 3(x + 2)     = (x + 2)(m + 3) -1(x + 2) = (x + 2)[(m + 3) – 1]
                                                = (x + 2)(m + 3 – 1)

Otra forma de hacerlo

m(x + 2) – x – 2 + 3(x + 2)     = m(x + 2) -1(x + 2) + 3(x + 2) = (x + 2)(m + 3 -1)

 

 

TRINOMIO CUADRADO PERFECTO

Se llama trinomio cuadrado perfecto al trinomio (polinomio de tres términos) tal que, dos de sus términos son cuadrados perfectos y el otro término es el doble producto de las bases de esos cuadrados.

En el trinomio cuadrado perfecto los términos cuadrados son siempre positivos, en cambio el término del doble producto puede ser negativo; en este caso debe ser negativo uno de los términos del binomio cuyo cuadrado es el trinomio dado, del ejemplo anterior tenemos:

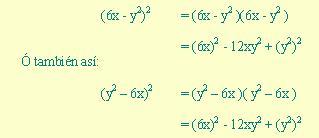
Ambas son respuestas aceptables.

Regla para conocer si un trinomio es cuadrado perfecto

Un trinomio ordenado con relación a una letra es cuadrado perfecto cuando la primera y tercer letra son cuadrados perfectos (o tienen raíz cuadrada exacta) y son positivos y el segundo termino es el doble producto de sus raíces cuadradas.

Ejemplos:

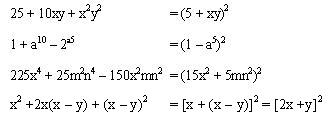
CREACION DE TRINOMIOS CUADRADOS PERFECTOS

Existe una manera de lograr trinomios cuadrados perfectos a partir de binomios si simplemente les sumamos y restamos el termino que le haga falta.

1. Si tenemos un binomio cuyos dos factores tengan raíces cuadradas se siguen los siguientes pasos para la creación de un trinomio cuadrado perfecto:

 

•  

  • Se les extrae la raíz cuadrada a los dos términos.

  • Se encuentra el doble producto de estas raíces.

  • Este doble producto se suma y se resta a los dos términos que son cuadrados perfectos.

Ejemplo:

 

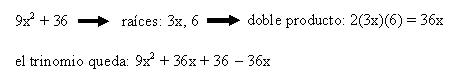
1. Si tenemos un binomio de la forma x2 + bx hace falta completarlo con el cuadrado de la mitad del coeficiente de la raíz del termino de la derecha.

Ejemplo:

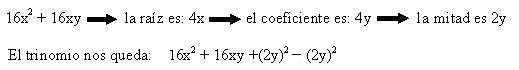
Pero para que el resultado original del polinomio no varie se le debe restar lo mismo q

TRINOMIO CUADRADO DE LA FORMA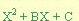 

Este tipo de trinomio tiene las siguientes características:

• Tienen un termino positivo elevado al cuadrado y con coeficiente 1 ().

• Posee un termino que tiene la misma letra que el termino anterior pero elevada a 1 (bx) (puede ser negativo o positivo).

• Tienen un termino independiente de la letra que aparece en los otros dos (+ o -).

Reglas para factorizar un trinomio de esta forma:

1. Se descompone el trinomio en dos factores binomios cuyo primer termino será la raíz cuadrada del termino .

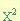1. El signo del primer binomio será el mismo signo que tenga el termino “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.

1. Si los dos factores tienen signos iguales entonces se buscan dos números cuya suma sea igual que el valor absoluto del factor “b” de “bx”, y cuyo producto sea igual al valor absoluto del factor “c”, estos números son los segundos términos de los factores binomios.

1. Si los dos factores tienen signos diferentes entonces se buscan dos números cuya diferencia sea igual que el valor absoluto del factor “b” de “bx”, y cuyo producto sea igual al valor absoluto del factor “c”, el mayor de estos números será el  segundo término del primer factor binomio, y el menor de estos números será el  segundo término del segundo factor binomio.

Ejemplo explicativo:

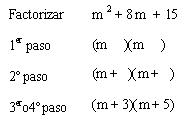
Ejemplos:

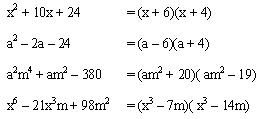
Detengámonos un poco en los últimos dos ejemplos. 

En el tercero podemos ver que lo que hemos llamado “x” no es una sola letra, pero aun así se utiliza el mismo procedimiento, esto es porque el “x” es un factor lo que implica que no necesariamente será una simple letra, este puede ser también un polinomio completo.

Siguiendo con el tercero vemos su cantidad numérica es bastante elevada y no todos pueden ver fácilmente los números que buscamos, una herramienta bastante útil es descomponer este numero en sus factores primos, de esta manera sabemos que cualquier combinación que hagamos al multiplicar estos números para formar los dos  que busco cumplirán con el requisito multiplicativo y solo me preocupare por cumplir la suma algebraica.  Así:

En el cuarto ejemplo se observa que el termino “c” no es un simple numero sino que tiene una forma 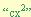, en este caso no se ha hecho ninguna diferencia simplemente se a tomado como factor “b” como si fuera “21m” así al multiplicar (7m)(14m) nos resulta  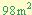 y al sumar 7m + 14m nos da 21m, con lo que se cumple con los requisitos.

Los términos “x”, “b” y “c” pueden ser cualquier cosa, ya sea números, letras, o polinomios , solo se necesita que se cumplan las reglas indicadas.

TRINOMIO DE LA FORMA 

Este tipo de trinomio se diferencia del anterior debido a que el termino al cuadrado (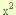) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo).  Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:

1. Multiplicamos el coeficiente “a” de el factor “a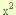” por cada termino del trinomio, dejando esta multiplicación indicada en el termino “bx” de la manera “b(ax)”, y en el termino “a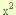” de la manera .

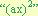1. Se descompone el trinomio en dos factores binomios cuyo primer termino será la raíz cuadrada del termino 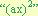 la que seria “ax”.

1. al producto resultante lo dividimos entre el factor “a”, con el fin de no variar el valor del polinomio.

1. El signo del primer binomio será el mismo signo que tenga el termino “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.

1. Se buscaran los segundos términos de los binomios según los pasos tres y cuatro del caso del trinomio anterior.

Ejemplo explicativo:

Ejemplos:

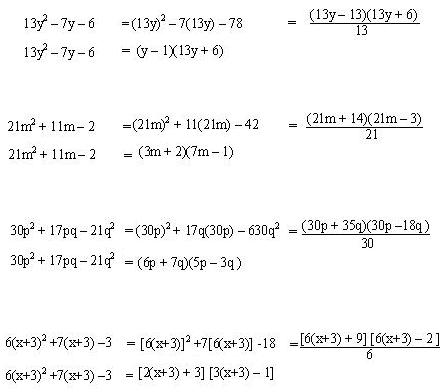
Siempre que sea posible hay que realizar la división indicada que nos queda de este tipo de trinomio, sin olvidar que cada factor del denominador que se simplifique se corresponde (2.3.5) a todos los términos de uno solo de los binomios.

DIFERENCIA DE CUADRADOS

Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta.

Al estudiar los productos notables teníamos que:

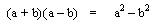
En donde el resultado es una diferencia de cuadrados, para este capitulo es el caso contrario:

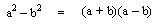
Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de sus bases.

Pasos:

1. Se extrae la raíz cuadrada de ambos términos.

1. Se multiplica la suma por la diferencia de estas cantidades (el segundo termino del binomio negativo es la raíz del termino del binomio que es negativo).

Ejemplo explicativo:

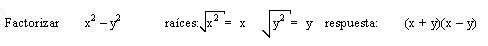
Ejemplos:

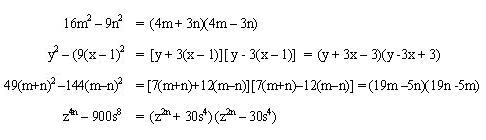
DIFERENCIA DE CUADRADOS

Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta.

Al estudiar los productos notables teníamos que:

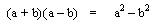
En donde el resultado es una diferencia de cuadrados, para este capitulo es el caso contrario:

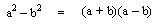
Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de sus bases.

Pasos:

1. Se extrae la raíz cuadrada de ambos términos.

1. Se multiplica la suma por la diferencia de estas cantidades (el segundo termino del binomio negativo es la raíz del termino del binomio que es negativo).

Ejemplo explicativo:

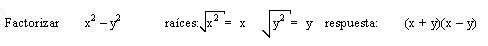
Ejemplos:

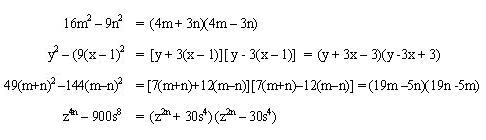
CUATRINOMIO CUBO PERFECTO DE BINOMIOS

De los productos notables tenemos:

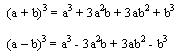
En este caso la factorización es realizar la operación inversa a esta:

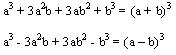
Para reconocerlo se deben tomar en cuenta los siguientes puntos.

• Debe tener cuatro términos, y estar ordenado con respecto a una letra.

• Dos de sus términos, el 1º (a) y el 4º (b), deben poseer raíz cúbica exacta.

• El segundo termino debe ser igual al triple producto del cuadrado de la raíz cúbica del primer termino por la raíz cúbica del cuarto termino [3(a)(b)].

• El tercer termino debe ser igual al triple producto de la raíz cúbica del primer termino por el cuadrado la raíz cúbica del cuarto termino [3(a)(b)].

• El segundo y el cuarto termino deben tener el mismo signo y puede ser positivo o negativo, el primer y tercer termino siempre son positivos (si el primer y tercer termino son negativos realizar factor común con el factor -1).

• Si todos los términos son positivos el resultado es el cubo de la suma de dos cantidades (a + b), si hay términos negativos el resultado es el cubo de la diferencia de dos cantidades (a – b).

Ejemplo explicativo:

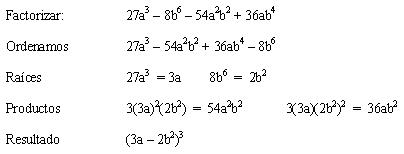
Ejemplos:

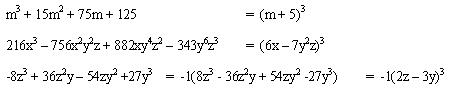
En este tipo de factoreo, se trata de reconocer que pertenece a este tipo polinomio.

SUMA O DIFERENCIA DE CUBOS PERFECTOS

Recordamos de cocientes notables que:

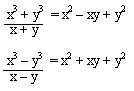
Pero en la división exacta el dividendo es igual al divisor multiplicado por el cociente, efectuándolo nos queda:

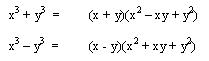
De donde se deducen las siguientes reglas:

• La suma de dos cubos perfectos se descompone en dos factores, el primero es la suma de sus raíces cúbicas, y el segundo se compone de el cuadrado de la primera raíz menos el producto de ambas raíces más el cuadrado de la segunda raíz.

• La diferencia de dos cubos perfectos se descompone en dos factores, el primero es la diferencia de sus raíces cúbicas, y el segundo se compone de el cuadrado de la primera raíz más el producto de ambas raíces mas el cuadrado de la segunda raíz.

Ejemplo explicativo:

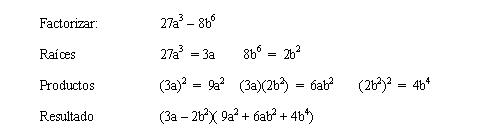
Ejemplos:

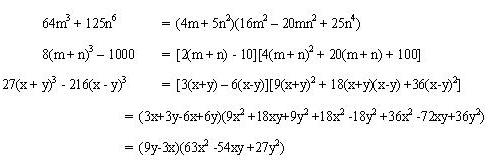
SUMA O DIFERENCIA DE DOS POTENCIAS IGUALES

 

De los cocientes notables recordamos que:

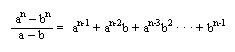
Pero en la división exacta el dividendo es igual al divisor multiplicado por el cociente, al despejarlo nos queda:

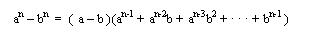
Y esto es valido para cualquier diferencia de dos potencias iguales ya sean impares o pares.

 

Así también:

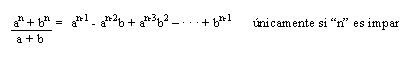
Al Despejarlo nos queda:

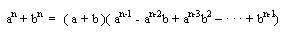
Que es valido para cualquier suma de dos potencias iguales impares únicamente(con pares no funciona).

 

Si tomamos también:

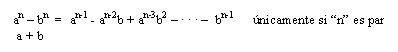
Al Despejarlo nos queda:

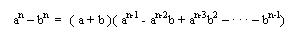
Que es valido para cualquier diferencia de dos potencias iguales paresúnicamente (con impares no funciona).

 

PASOS PARA FACTORAR LA SUMA O LA DIFERENCIA DE DOS POTENCIAS IGUALES

Pasos:

1. Clasificar la expresión en positiva o negativa, y en par o impar (si son positivas y pares no se pueden realizar por este método).

1. Se sacan las raíces de cada termino.

1. Se coloca el primer factor el cual es un binomio cuyo primer termino es la raíz del primer termino dado y el segundo termino es la raíz del segundo termino dado.

1. El signo del primer factor (binomio) será el mismo que tiene la expresión dada.

1. Se crea el segundo factor (un factor polinomio) en el cual existirá un número de términos igual al exponente de la expresión dada (los siguientes pasos son solo para el segundo factor).

1. En cada término se multiplicara el término de la izquierda por el término de la derecha de la expresión dada

1. En el primer término del factor polinomio el factor de la izquierda tendrá un exponente igual a “n – 1”, y el factor derecho tendrá un exponente de cero.

1. Para los exponentes de los siguientes términos, en el caso del factor de la izquierda irán disminuyendo en una unidad, y los del termino de la derecha irán aumentando también en una unidad (si se suman los exponentes de los dos términos siempre será igual a n-1).

1. Si el binomio es negativo todos los términos del polinomio son positivos, si el binomio es positivo impar los signos del polinomio se alternarán (+ ó –) comenzando por el “+”.

1. Cuando en el polinomio, el exponente del termino de la derecha sea igual a n-1 damos por terminada la respuesta.

Ejemplos explicativos:

Ejemplos:

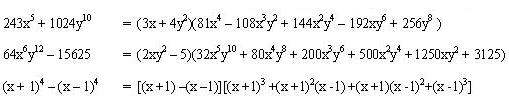
Al igual que en los demás casos un factor es cualquier cosa ya sea un numero una letra una combinación de números y letras y operaciones.

ECUACIONES

La intensión de resolver las ecuaciones es encontrar sus raíces o soluciones de la ecuación.

Lo primero que hay que saber es que toda ecuación algebraica de grado n con coeficientes reales o complejos tiene al menos una raíz real o compleja. Este enunciado es el teorema fundamental del álgebra.

D'Alembert fue el primer matemático que dio una demostración, pero no era completa. Se considera a Gauss como el primer matemático que dio una demostración rigurosa.

Conceptos básicos:

Igualdad:        Es la expresión en la cual se indica que una expresión tiene el mismo valor que otra. La igualdad sólo se cumple para determinados valores de la expresión.

                                   5 + 10 = 3*5               2m +8 = 12                

Identidad:       Es la expresión en la cual se indica que dos expresiones son iguales para cualquier valor que se ponga en lugar de las letras que figuran en la expresión

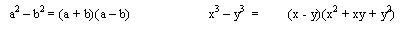
Ecuacion:       Es la expresión de igualdad condicionada por cantidades conocidas y cantidades desconocidas o incógnitas, que se cumplen únicamente para determinados valores. Las ecuaciones son igualdades.  Nunca debemosolvidar esto.

                                   Y -2 = 6                      se cumple si     Y = 8

                                   3x + 5y = 23y              se cumple si     x = 6y

Miembros:      miembros de una ecuación son las expresiones colocadas a la derecha y a la izquierda del signo igual (=)
.

                                  3x = 5              donde 3x es el primer  miembro y 5 el segundo miembro.

Términos:       términos de una ecuación, son cada una de las expresiones que estan conectadas con otra por los signos de suma y resta (+, –).

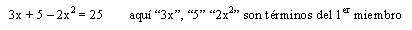
Grado:           el grado de una ecuación con una incognita es el mayor exponente de esa incognita.

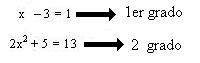
Raíz:                se le llama raíz de una ecuación a cualquier valor numérico que al sustituirse por la incógnita satisfaga la ecuación.

                        3x = 15            la raíz es 5 pues 3(5) = 15 y cumple la condición.

Conjunto solución:     es el conjunto de todos los números que satisfacen la igualdad en una ecuación. Es el conjunto de todas las raíces de la ecuación.

            3x2 = 12        {2, -2} son el conjunto solución pues ambos cumplen la condición

Debemos distinguir entre identidades y ecuaciones. Cuando dos expresiones son iguales para cualesquiera valores que se pongan en lugar de las letras que figuran en la expresión es una identidad. Cuando la igualdad sólo se cumple para determinados valores de la expresión es una ecuación.

comprobación de ecuaciones:  la comprobación se realiza sustituyendo la raíz obtenida en la ecuación original, si ambos miembros dan el mismo resultado se confirma la respuesta.

CLASIFICACIÓN

Las ecuaciones se pueden clasificar de varias formas: 

Por el número de incógnitas. 

Las ecuaciones pueden tener una o más incógnitas. Por ejemplo la ecuación 3x + 4 = 10, sólo tiene una incógnita, la ecuación 3x - y = 5, tiene dos y 5xy - 3x2 + z = 8 tiene tres incógnitas.

Las ecuaciones con una incognita se pueden imaginar como puntos sobre el eje x. Las de dos incógnitas como curvas en un plano. Las de tres incógnitas como curvas en un espacio de tres dimensiones.

Por el grado de la incógnita.

Las ecuaciones de una incógnita se pueden clasificar por el grado de la incógnita (el grado es el exponente más alto de la incógnita).

Si el exponente mas alto es uno entonces la ecuación es de primer grado.

Si el exponente mas alto es dos entonces la ecuación es de segundo grado o cuadrática.

Si el exponente mas alto es tres entonces la ecuación es de tercer grado o cúbica. Y así sucesivamente.

Hay fórmulas generales para resolver las ecuaciones de grado 1 a 4 (pero las fórmulas son complicadas y difíciles de recordar para grado mayor que 2). Si no se puede descomponer la ecuación en factores, cualquier ecuación, sea del grado que sea, se puede resolver de esta forma: 

                        Sea la ecuación: xn + a1xn-1 + a2xn-2 + ... + an = 0
                        Si x1, x2, ..., xn son las soluciones de la ecuación, se cumplen las siguientes ecuaciones:
                        x1 + x2 + ... + xn = -a1 
                        x1x2 + x1x3+...+x1xn + x2x3+...+ x2xn + ...+ xn-1xn = a2 
                        x1x2x3 + x1x2x4 + ...+ x1x2xn + x2x3x4 +...+ x2x3xn + ...+ xn-2xn-1xn = -a3
                        ..................................
                        x1x2...xn = (-1)nan

Utilizando estas ecuaciones, tendríamos un sistema de ecuaciones que nos permitiría obtener las soluciones.

Por el número de términos

Ecuaciones binómicas:

Las ecuaciones con dos términos se llaman ecuaciones binómicas.

Ecuaciones polinómicas:

Las ecuaciones que tienen tres términos, se llaman trinómicas, y aunque podríamos seguir llamándolas en función del número de términos, se suelen llamar polinómicas.

De acuerdo a su conjunto solución

Ecuación identidad:               es la que se cumple para cualquier valor de la variable.

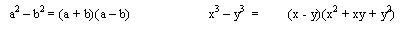
Ecuación condicionada:        es cuando se le añade a la ecuación una condición adicional.

            5x + 2y = 9   tal que “x” y “y” pertenecen a N;            la pertenencia a los números Naturales es la condición.

Ecuaciones equivalentes:       cuando el conjunto solución de una ecuación es igual al de otra ecuación se dice que estas ecuaciones son equivalentes.

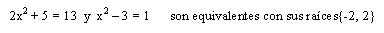
Por su estructura

Ecuación entera:                    es aquella en que todos sus términos son enteros.

                        6y + 4x – 5 = 3x – 2 ;             2x – 3y = 9

Ecuación fraccionaria:          es aquella en que uno o mas de sus términos poseen denominador.

                        x  + 5y – 2 = 3x + 1 ;              12  +  3  =  5x
                        5             3     2                         x       y

Ecuación racional:                 es en la que ninguno de sus términos lleva la incógnita bajo un radical.

                        2x – 3y = 9 ;                √2 – 5m√32 = 7
                                                             x

Ecuación irracional:             es en la que al menos uno de sus términos lleva la incógnita bajo un radical.

                        2√x – 3y = 9 ;             √x – 5m√m = 7 - m

ECUACIONES LINEALES

Las ecuaciones de la forma ax + b = 0 son muy sencillas de resolver, basta con despejar la x.

Despejar la x significa dejar la x sola a un lado del signo igual. Para pasar un número, o una variable, al otro lado del signo igual tenemos que seguir estas reglas:

• Si está sumando pasa restando y si esta restando pasa sumando. En nuestro caso quedaría ax = -b

• Si está multiplicando pasa dividiendo y si está dividiendo pasa multiplicando. En nuestro caso x = -b/a.

Una forma más sencilla de ver este método de despejar, es que a los dos miembros de las ecuaciones se les realizan exactamente las mismas operaciones a cada uno.  Como son iguales, el uno y el otro, al realizarles exactamente la misma operación su resultado variara exactamente de la misma manera (en el caso que sea cero un multiplicando o un dividendo esta regla no se aplica).

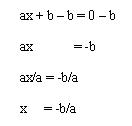
Pasos:

1. Se efectúan las operaciones indicadas de cada miembro, si las hay.

1. Se añaden los mismos términos a cada lado del igual a fin de dejar todas las expresiones con incógnita de un lado de la ecuación y todas las cantidades conocidas del otro lado.

1. Se reducen los términos semejantes.

1. Se despeja la incógnita dividiendo entre el coeficiente de la incógnita ambos miembros de la ecuación.

1. Se comprueba que el resultado obtenido sea correcto reemplazándolo en la ecuación original.

Ejemplo explicativo:

Existen muchas ecuaciones que a simple vista se puede suponer que son de un grado superior pero que fácilmente se convierten en ecuaciones de 1er grado al factorizar ó añadir términos para desaparecer los términos de grado superior a uno.

Ejemplo explicativo:

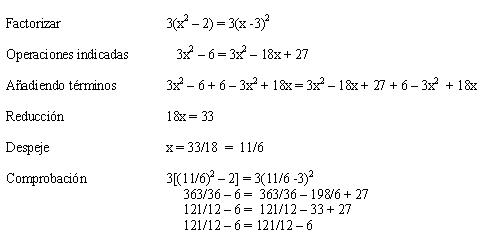
Ejemplos:

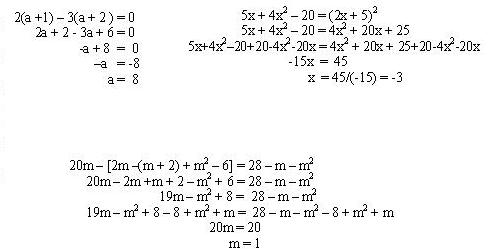
ECUACIONES CUADRATICAS

Una ecuación cuadrática es una ecuación de segundo grado cuya forma estándar es:

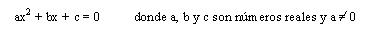
método de factorización

Una técnica importante para resolver educaciones cuadráticas tiene como base el hecho de que si “m” y “n” son factores reales, tales que pq = 0, entonces p = 0 ó q = 0, de ahí que si 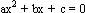 puede expresarse como un producto de polinomios de primer grado, entonces pueden encontrarse soluciones igualando cada factor a cero.

Si una ecuación cuadrática puede ser factorizada en una multiplicación de factores lineales, entonces puede decirse que es una ecuación factorizable.

Por ejemplo:

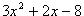
Es una ecuación factorizable porque puede ser factorizada por los factores lineales (3x - 4) y (x + 2). O sea:

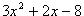= (3x - 4)(x + 2).

Para resolver una ecuación mediante este método se siguen los siguientes pasos

1. Primero se escribe la ecuación en la forma .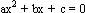

2. Luego se factoriza la expresión en factores lineales

3. Se iguala cada factor a cero

4. Se determina el valor de x .

Ejemplo:

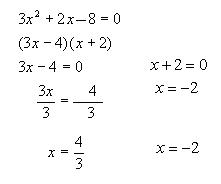
Las raíces son 4/3 y -2 y cualquiera de ellas cumple exactamente la ecuación.

Las técnicas de factoreo vistas anteriormente son usadas en gran medida en este tipo de ecuaciones.

FORMULA CUADRATICA

Cuando la ecuación cuadrática está en su forma estándar y se nos hace difícil encontrar sus raíces mediante factorización, podemos utilizar el método de la fórmula cuadrática.

La fórmula cuadrática es:

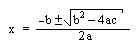
Pasos para Buscar las Raíces de una Ecuación Usando la Fórmula Cuadrática:

1. Llevar a la ecuación a su forma estándar

1. Determinar los valores de las constantes a, b y c.

1. Utilizar la fórmula cuadrática sustituyendo los valores por las variables, primero con el signo “+” para encontrar una raíz y luego con el signo “-” para encontrar la segunda raíz.

Ejemplo:

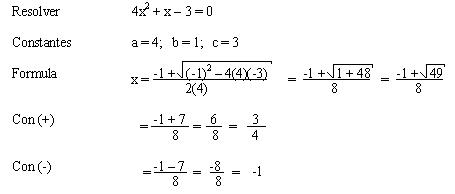
DESIGUALDADES

Una inecuación o desigualdad es lo mismo que una ecuación pero cambiando el signo de igualdad por signo(s) de desigualdad.

Los signos de desigualdad son

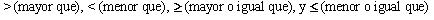
 Para resolver una desigualdad lineal se utilizan los mismos pasos que se usan para resolver una ecuación lineal. Como ejemplo, vamos a resolver la desigualdad

                        3 > x - 8.

Sumando la misma cantidad a ambos lados:

                        3 > x - 8
3 + 8 > x - 8 + 8
11 > x

Una regla importante en las desigualdades es que cuando se multiplica o divide por un número negativo, el signo de desigualdad cambia.

Ejemplo:

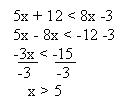
Normalmente la respuesta de una desigualdad se encuentra desde un numero hasta llegar a otro numero, contando a todo numero que se encuentre en medio de estos, esto normalmente es conocido como un intervalo (seran estudiados en la siguiente leccion).

Desigualdades que Envuelven Dos Posibles Soluciones

Hay desigualdades que envuelven dos posibles soluciones, una positiva y otra negativa. 

Por ejemplo:

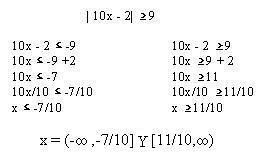
También existen sistemas de dos o mas inecuaciones con respuestas iguales estas se trabajan igual que los sistemas de ecuaciones, cuyas reglas veremos en el capitulo 43.

SISTEMAS DE ECUACIONES

Se llama sistema de ecuaciones todo conjunto de ecuaciones distintas que tiene una o más soluciones comunes.

Resolver un sistema de ecuaciones simultáneas es hallar el conjunto de valores que satisfacen simultáneamente cada una de sus ecuaciones.

Características de un sistema de dos ecuaciones lineales con dos incógnitas.
Los resultados característicos de resolver un sistema de dos ecuaciones lineales con dos variables son:

Un sistema es consistente si tiene por lo menos una solución. Un sistema con un número infinito de soluciones es dependiente y consistente. Un sistema esinconsistente si carece de solución.

Para resolver un sistema de N ecuaciones con N incógnitas podemos utilizar uno de los siguientes métodos:

Sustitución 
Igualación 
Reducción

Método de sustitución

Sea el sistema

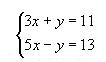
Primero en una de las ecuaciones se halla el valor de una de las incógnitas. despejemos la y en la primera ecuación suponiendo como conocido el valor de x

y  =  11 - 3x

Se sustituye en la otra ecuación el valor anteriormente hallado, es decir donde se encuentre una "y" colocaremos "(11 – 3x)".

5x - (11-3x)  =  13

Ahora tenemos una ecuación con una sola incógnita; la cual resolvemos normalmente

5x – 11 + 3y  =  13
5x + 3x  =  13 + 11
8x  =  24
x  =  3 

Ya conocido el valor de x lo sustituimos en la expresión del valor de "y" que obtuvimos a partir de la primera ecuación del sistema

y  =  11 - 3x
y  =  11 - 9
y  =  2

Así la solución al sistema de ecuaciones propuesto será x=3 e y=2

Método de igualación

Sea el sistema  

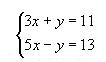
Lo primero que haremos será despejar en las dos ecuaciones la misma incógnita

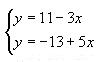
Igualamos ambas ecuaciones

11 - 3x  =  -13 + 5x
8x  =  24 
x  =  3

Este valor de x lo sustituimos en cualquiera de las ecuaciones de y

y  =  11 - 9
y  =  2

Método de reducción

Sea el sistema

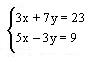
Sumaremos miembro a miembro las dos ecuaciones que componen el sistema, la intención es eliminar una variable por lo que si no se puede eliminar ninguna así nomás se multiplicaran las ecuaciones por números que igualen alguno de los términos, para que se elimine uno:

Para este ejemplo eliminamos "y"

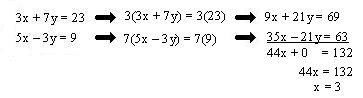
y sustituyendo este valor en cualquiera de las ecuaciones del sistema obtenemos

y = 2

Este método sirve para cualquier cantidad de ecuaciones con la única condición que el numero de variables desconocidas no sea mayor a la cantidad de ecuaciones.